Effects of Measurement Error
Distributions
Theoretically, the use of data from an instrument affected only by [glossary term:] within-person random error leads to an estimated population distribution of usual intake that is too wide compared to the true usual intake distribution due to excess within-person random error (Figure 2).
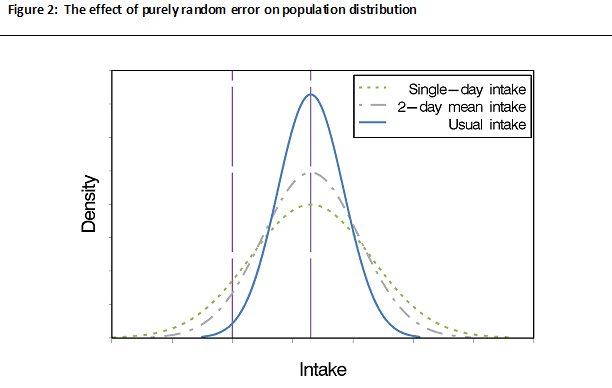
As Figure 2 shows, a distribution of intakes for a population based on intakes for a single day (e.g., a single 24HR or food record) is wider and flatter compared to the usual intake distribution. The figure, which assumes the data are affected by [glossary term:] random error only with no systematic error, also shows that averaging over two days of intake data (i.e., 2-day mean intake) may somewhat dampen the effects of within-person random error but is not sufficient to fully remove its effects.
An important implication is that if the within-person random error is not appropriately adjusted for, erroneous conclusions may result. For example, the estimate of the fraction of a population of interest with usual intake above or below some standard, such as a nutrient requirement or food group recommendation, may be incorrect. This is because without accounting for within-person random error, the probabilities in the tails of the distribution are overestimated.
It should be noted that if data are affected by within-person random error only, the population mean based on a single day's report is equal to the [glossary term:] mean population usual intake so long as the data are reasonably randomly distributed across seasons and days of the week (Learn More about Day-of-Week Effects and Learn More about Season Effects). Thus, it is not necessary to account for within-person random error if one is interested in estimating only mean usual intake rather than some other feature of the distribution, such as the proportion above or below a threshold.
The use of data from an instrument with [glossary term:] systematic error (with or without within-person random error) leads to an estimated distribution of usual intake that has a different mean and shape than the true usual intake distribution (Figure 3). This also can lead to erroneous conclusions, such as a biased estimate of the fraction of a population with usual intake above or below some standard, such as a nutrient requirement or food group recommendation. In addition, the population's mean [glossary term:] self-reported intake will be a biased measure of the true population mean intake (in contrast to the situation in which the data are affected only by within-person random error).
In practice, data from instruments, such as 24HRs, that capture dietary intake with less [glossary term:] bias relative to other instruments are preferred for estimating mean usual intake among populations and subpopulations (see Choosing an Approach for Dietary Assessment). Although the resulting means are likely affected by some bias, they represent the best possible estimates in the absence of [glossary term:] reference instruments for most dietary components.

Regression Models
The effects of measurement error on estimates derived from regression models depend on the study objective (e.g., whether the diet is the [glossary term:] exposure or the [glossary term:] outcome).
In the case in which diet is the exposure of interest in relation to some outcome such as health or disease, whether the models include one or more dietary exposures is an important factor in determining the effects of measurement error. When a single dietary exposure is measured with within-person random error only (i.e., without systematic error), the estimate of the [glossary term:] association between the exposure and the health or disease outcome is always attenuated (i.e., biased toward the null). In addition, within-person random error causes a loss of power to detect relationships between a single dietary exposure and an outcome, meaning that a larger sample size is needed to detect a relationship that actually exists. However, in the case of within-person random error only, the statistical test of no association of the health outcome with the dietary exposure is valid (i.e., the probability of the [glossary term:] null hypothesis being rejected when it is in fact true, known as Type I error, is controlled at the specified level).
When a single dietary exposure contains both systematic and within-person random error, the estimate of the association with the outcome may be biased in either direction from the null, i.e., it may be attenuated or inflated. This is because person-specific bias and within-person random error attenuate the association, whereas intake-related bias, when manifested as a flattened slope, exaggerates the association.
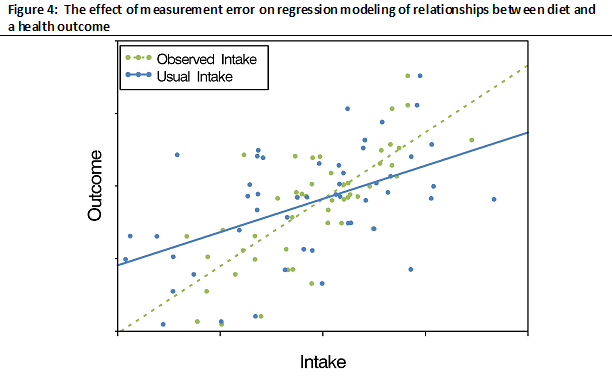
The typical structure of measurement error in data collected using self-report dietary assessment instruments is such that the effects of person-specific bias and within-person random error predominate over the effects of intake-related bias, leading to overall [glossary term:] attenuation (Figure 4). Furthermore, the statistical test of no association remains valid. The loss of statistical [glossary term:] power to detect diet-health outcome associations that occurs with within-person error is exacerbated by the presence of systematic error, including person-specific bias.
When a health outcome model contains other dietary [glossary term:] covariates (nutrients or food groups) in addition to the main dietary exposure of interest, the effects of measurement error are less predictable than with a single dietary exposure. This is because the estimated association between the main dietary exposure and the outcome may be attenuated or inflated because of possible [glossary term:] residual confounding with other dietary covariates also measured with error. Furthermore, the statistical test of the main exposure association may not be valid, that is, there is increased probability that the null hypothesis will be rejected when it is in fact true (Type I error).
Assessing the effects of interventions on dietary outcomes also is complicated by measurement error. The use of data affected by measurement error can result in biased estimates of intervention effects and loss of power to detect them, even when the intervention and control groups misreport intakes to the same extent.
Further, in intervention studies, the intervention itself may change both reporting and [glossary term:] true intake, making interpretation particularly difficult. The resulting [glossary term:] differential error in reporting of intakes among groups can lead to spurious results. For example, if the intervention group under-reports fat intake to a greater extent than the control group, spurious estimates of the effect of the intervention on fat intake can occur. Similar problems can occur in studies examining relationships between dietary outcomes and other variables (e.g., socioeconomic status) that might be associated with both reporting of intakes and true dietary intake.
| Type/Subtypes of Measurement Error | Effects | Ways to Address Effects |
|---|---|---|
| Systematic Error/Bias | Inaccuracy: biased estimates of mean and distribution | Use of reference instrument, such as [glossary term:] biomarker, or less-biased instrument |
| Intake-related (flattened slope) | Exaggerated relationships | |
| Person-specific | Attenuated relationships Loss of Power |
|
| Within-Person Random Error | Imprecision: estimates scattered around true value Distributions too wide, leading to overestimations of tail probabilities Attenuated relationships Loss of power |
Averaging repeat observations, or statistical modeling if number of repeats is limited |
